Poking with Probability

 

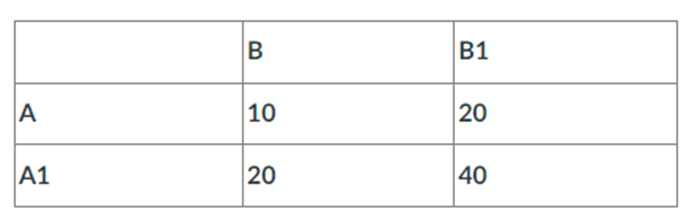
A1. For Event A, both values in the row for it add up to 30. Dividing this by the total value of 90 for all the listed data gives us a 1 in 3 chance of Event A occurring.

A2. The values in the B column, much like the row A, also add up to 30. Dividing by the total of 90 gives us a 1 in 3 chance of Event B occurring.

A3. To get the probability of either Event A or Event B occurring, we need to add the probabilities of both occurring together, and subtract that from the probability of both occurring at the same time. So, 1 of 3 plus another 1 of 3 (1/3 + 1/3) is equal to 2 of 3 (2/3). Now, to get the probability of both events occurring, we multiply both probabilities together (1/3 * 1/3), which gives us 1/9. 2/3 can be rewritten as 6/9, and subtracting the 1/9 probability of both events occurring leaves us with 5/9, or a roughly 56% chance of either Event A or Event B occurring.

A4. As noted in the previous question the probability of A plus the probability of B (1/3 + 1/3) is equal to 2/3, so there’s a rough 66% chance of A or B occurring.

B. The answer to this equation is TRUE; there is a rough 11% chance of rainfall on the day of Jane’s wedding. As for why this is true, we need only refer to how much B is influenced by both A2 and A1. A1 (there being rain) spurs a prediction that’s accurate about 90% of the time, while A2 gives us a low accuracy of 10%, with rainfall being rare. Since P( A1 | B ) is properly calculated to be 11%, this brings us very close to our P( B | A2 ) value of 0.1, confirming that the chances of rain on Jane’s wedding very minimal.

C.